Nächste Seite: Euler Tour und Matrize Aufwärts: Übungen Vorherige Seite: Das folgende
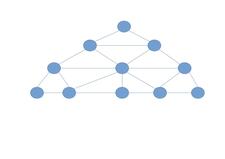
Fast trianguliert
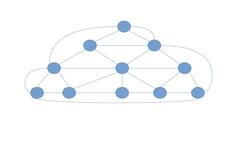
Vielleicht koennte man wie beim Pascallschen Dreieck die Knoten mit ganzen Zahlen fuellen die die Summen der vorherigen sind Oder man koennte Beweisen, dass dreiecke zusammen wieder Dreiecke bilden

Ich habe was induktives fuer Graphen: Tiefen und Breitensuche sind Induktiv, aber wie soll man oder was soll man da beweisen?
Ich mache jetzt keine Rechenaufgaben mehr, kein Handschriftliches Rechnen, nichts, aber ich mache Eulertouren, aber Matrizenmultiplikation mache ich
Vor allem muss ich darauf achten, dass ich die Graphen mathematisch Korrekt Hinschreibe, mit Mengen
Dann mache ich auch Tiefen und Breitensuche, mit Mengen und Tupeln
Neu, ist fuer mich der 5 Farben Satz ich habe ihm im Grossen uind Ganzen verstanden, zumindest eine Vorstellung davon
Ich weiss, was man die Menge

ist, das ist die Menge von Farben fuer einen Knoten

Dann gibt es die Farb-Liste
Das ist die Vereinigung aller aller

Und die Listenchronomatische Zahl, das ist

Gut, ich lerne da paar Saetze auswendig, etwa, dass die Listenchronomatische Zahl im Dreieck nicht groesser als 3 sein muesste. Drei wuerde genuegen
Das kann man ja lernen, ebenso mit der Listenchronomatischen Zahl usw.
Wenn man das hat, kann - und das sind neue uebungen von mir - neue Uebungen, das ist nicht auswendig lernen
Ich hoffe das hilft. Wer immer triangulierte Graphen zeichnet, wird sich nachher nicht schwer tun, sie wieder zu erkenen und sie zu benutzen, damit fange ich jetzt an
An der Stelle finde ich lernen besser als verstehen, ich weiss zum Beispiel nicht, warum er ueberhaupt von Triangulierten Graphen ausgeht
Gut, ich kann mir das so erklaeren, ich habe mir den Fast Triangulierten angeschaut. Wuerde ich noch mehr Kanten einfuegen, dann waere er nicht mehr planar.
Ich vermute, dass Trianguliert am Ende bedeuten wuerde, es waere die Maximale Valenz fuer jeden Knoten
Aber das ist mir egal, ich lerne den Beweis so, wie er da steht auswendig und alle Unklarheiten werden dann von alleine gehen.
Jetzt kommt Pause dann die Euler Tour und dann mache ich gleich die Tiefen und rein suche drin indem ich diesen mathematisch hinschreiben und dann mache ich das schon mal
So, jetzt kann ich bei den Uebungen auch gleich die Eulersche Polyeder Formel mitueben